Lami’s theorem, also known as Lami’s rule, is a principle in mechanics that explains the conditions for the equilibrium of three concurrent forces acting on an object. This theorem is named after Gabriel Lami, a French mathematician and physicist who first stated it in 1773. The theorem is used in engineering and physics to analyze the forces acting on an object in a three-dimensional space.
Statement of Lami’s Theorem
Lami’s theorem states that if three forces acting at a single point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces. Mathematically, the theorem can be written as:
F1/sin(α) = F2/sin(β) = F3/sin(γ)
where F1, F2, and F3 are the magnitudes of the three forces, and α, β, and γ are the angles between the forces, respectively.
Explanation of Lami’s Theorem
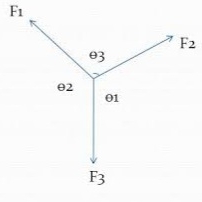
To understand the Lami’s theorem, let us consider a simple example. Suppose we have a point O, and three forces F1, F2, and F3 acting at this point, as shown in the figure below.
To determine whether these forces are in equilibrium, we can apply the Lami’s theorem. According to the theorem, if the forces are in equilibrium, then each force must be proportional to the sine of the angle between the other two forces.

Let us assume that the angle between F1 and F2 is α, the angle between F2 and F3 is β, and the angle between F3 and F1 is γ. Then we can write:
F1/sin(α) = F2/sin(β) = F3/sin(γ)
If we know the magnitudes of any two forces and the angles between them, we can use the above equation to calculate the magnitude of the third force. For example, if we know F1 and F2, and the angle between them α, we can calculate the magnitude of F3 using the equation above.
Applications of Lami’s Theorem
Lami’s theorem has several applications in physics and engineering. Some of these are discussed below:
1. Truss Analysis: Lami’s theorem is used to analyze the forces acting on the members of a truss structure. A truss is a structure that consists of a series of interconnected triangles. Each joint in the truss is subjected to three forces, and the Lami’s theorem can be used to analyze these forces.
2. Crane Stability: Lami’s theorem is used to analyze the stability of cranes. A crane is a machine that is used to lift heavy objects. The stability of a crane depends on the forces acting on the crane, and the Lami’s theorem can be used to analyze these forces.
3. Equilibrium of Three Forces: Lami’s theorem is used to determine whether three forces acting on an object are in equilibrium. For example, if we have three forces acting on a bridge, we can use the Lami’s theorem to determine whether the bridge is in equilibrium.
Lami’s theorem is a powerful tool in mechanics that is used to analyze the equilibrium of three concurrent forces. The theorem states that if three forces acting at a single point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces. The theorem has several applications in physics and engineering, including truss analysis, crane stability, and equilibrium analysis of three forces.

Leave a Reply